¶ Function
Elevation: The observations are weighted depending on the elevation of the specific satellite. You can define your own weighting function in the text field. Usually, sin²(e) is used. Please check str2func.m for the corresponding syntax and note that ‘@(e)’ is automatically added to the string from the GUI. Do not forget points to allow element-wise operations. Note that the elevation is considered in radiants. Weighting function examples (e.g., Hadas et al. 2020):
sin(e).^2
sin(e)
% exponential
1./(1+3.5.*exp(-180.*e/pi/9))
% cosin e -type
1./sqrt(1+4.*cos(e).^8)Multipath-LC: weights are calculated from the value of the Multipath-Linear-Combination. Check this article.
Signal strength: Weighting is based on the Carrier-to-Noise-Density (C/N0) of the measurements. When processing the IF LC, the C/N0 values of the first frequency are used for that. You can define your own weighting function in the text-field. Please check str2func.m for the corresponding syntax and note that ‘@(snr)’ is automatically added to the string from the GUI. Do not forget points to allow element-wise operations. Examples are:
10.^-(max([55-snr,0])./10)
10.^-(max([55-snr,0])./20)
% with some values for a and b:
a + b.*10.^(-snr/20)
% implemented hardcoded functions (check figure):
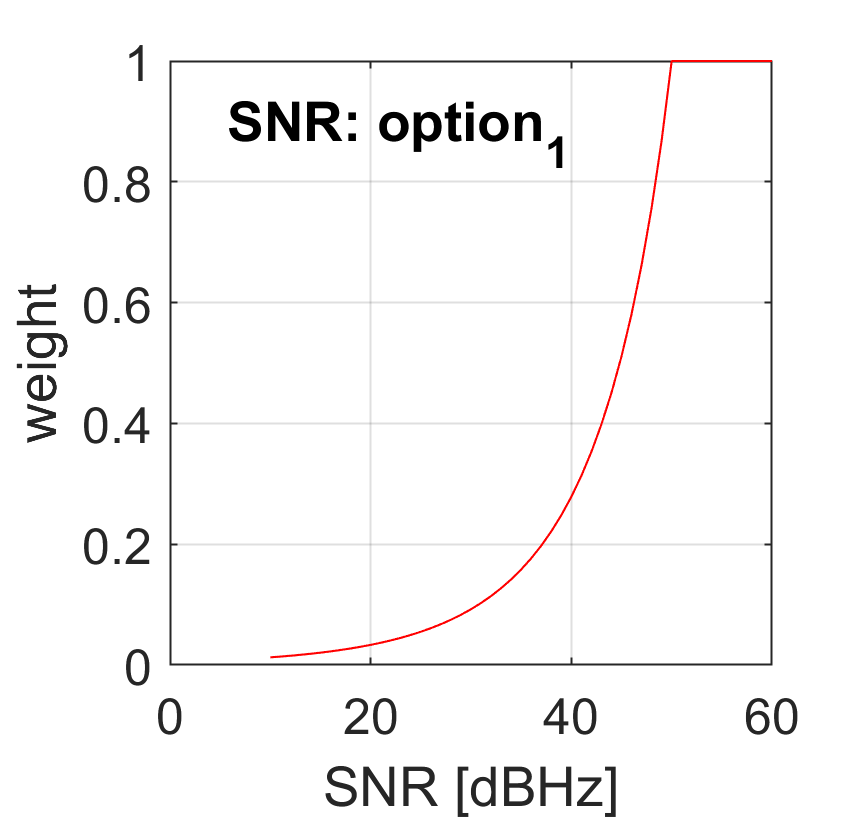
option_1
% simple linear function
-0.8.*SNR+37
None: all observations have the same weight (e.g., 1)
¶ GNSS Weights
Define a weight factor for the observations of each GNSS here, motivated by, for example, varying precision of the satellite orbits. The default value is 1 for all GNSS. An enormous value for a specific GNSS (e.g., 5) results in down-weighting, meaning that observation of this GNSS will less influence the solution. For example, giving BeiDou a weight of 2 will multiply the variance of the observations in the Kalman Filter by a factor of two.
¶ Standard deviation of raw observations
Define the standard deviation in the zenith direction of the code observations and the phase observations in [m]. When processing an IF LC, this raw standard deviation is increased during the processing due to the coefficients of the LC. Furthermore, the observation weighting function maps the defined standard deviation to the actual observation.
If the ionospheric delay is estimated with an ionospheric constraint, the standard deviation of the ionospheric pseudo-observations in the zenith direction is also defined here. Furthermore, the user can decide how long the ionospheric pseudo-observations should be used and to which level their standard deviation should be increased up to this point.
In addition to the defined standard deviation of the code and phase observation, the user can define frequency-specific standard deviations with the two provided tables. Missing values are replaced by the “regular” standard deviation of code and phase observation. Therefore, the “regular” standard deviation of code and phase observation are used during in the processing if both tables are kept empty.
Jump to Table of Content